Enunciado:

Tem comprador de papel velho...

Tilim, tilim...

Tilim, tilim...

Tocando o sininho

Por toda a cidade

Roda, roda a carrocinha.

Comprando notícias velhas,

Coisas vistas e revistas.

Caixas vazias de todas as formas:

redondas, quadradas, compridas,

que já embalaram brinquedos,

sapatos, bombons e camisas.

XAVIER, Marcelo. Tem de tudo nesta rua... São Paulo: Formato Editorial, 2010.

Quais os tipos de caixas são citados no poema? 

Faça uma ilustração dos tipos de caixas que você identificou no poema.

 A chamada Revolução Verde, iniciada na década de 1950, consistia em mudanças tecnológicas na produção agrícola e na reestruturação fundiária nos países subdesenvolvidos. Um dos objetivos dessas mudanças era resolver o problema da fome no mundo.

As consequências imediatas dessa revolução nos países subdesenvolvidos incluem

(UFPR) Em recente estudo, o IBGE (Instituto Brasileiro de Geografia e Estatística), com base em metodologia específica e analisando a distribuição, no espaço nacional, de variáveis relacionadas à gestão pública e à gestão privada, definiu os centros de gestão do território brasileiro. A tabela a seguir representa uma síntese dos resultados obtidos, com a classificação dos municípios por níveis de centralidade. 

Brasil: distribuição dos municípios por níveis de centralidade, 2014.

(Fonte: IBGE, 2014. Disponível: gestao_do_territorio/gestao_do_territorio_2014.pdf>. Acesso em 17 set. 2015)

Considerando os conhecimentos de geografia urbana e sabendo que no nível 1 de centralidade de gestão encontram-se São Paulo e Brasília; no 2, Rio de Janeiro; e no 3, Porto Alegre, Curitiba, Belo Horizonte, Salvador, Recife e Fortaleza, assinale a alternativa correta.

(IFCE) Se 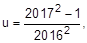 então é verdade que:

 Se ab = -6 e (4a² + b²) = 23, o valor numérico da expressão (2a + b)² é: