Um artesão fabrica vários tipos de potes cilíndricos. Mostrou a um cliente um pote de raio de base a e altura b. Esse cliente, por sua vez, quer comprar um pote com o dobro do volume do pote apresentado. O artesão diz que possui potes com as seguintes dimensões:

- Pote I: raio a e altura 2b

- Pote II: raio 2a e altura b

- Pote III: raio 2a e altura 2b

- Pote IV: raio 4a e altura b

- Pote V: raio 4a e altura 2b

O pote que satisfaz a condição imposta pelo cliente é o:

(FATEC) As tecnologias vestíveis digitais estão sendo incorporadas em mais e mais produtos que usamos no nosso cotidiano. Entre tantos, podemos citar exoesqueletos, relógios e óculos “inteligentes”, pulseiras fitness, lentes de contato para diabéticos, luvas de composição musical e realidade aumentada, unhas postiças eletrônicas, cílios postiços condutivos, sapatilhas de corrida eletrônicas e tatuagens digitais. Em virtude dessa crescente oferta, observa-se o acréscimo significativo de adeptos, comprovado pelo surgimento de revistas, congressos, conferências e exposições especializados sobre o tema. Enfim, uma revolução no modo de vida das pessoas.

Os tecidos animais descritos no quadro são formados por um conjunto de células especializadas, e a organização estrutural de cada um reflete suas respectivas funções.

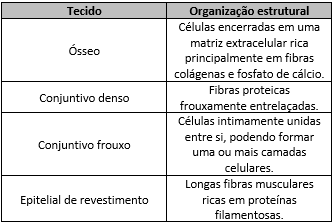
De acordo com a organização estrutural dos tecidos descrita, aquele que possui a capacidade de formar barreiras contra agentes invasores e evitar a perda de líquidos corporais é o tecido:

MEDEIA - (de dentro) Ai! Desgraçada de mim e dos meu males. Ai, ai de mim, que fim será o meu?

AMA - Vedes, caros filhos; a vossa mãe o peito se lhe agita e move a ira. Correi depressa para dentro do palácio, e não vos acerqueis da sua vista, nem vos aproximeis, mas defendei-vos do caráter selvagem, temeroso de um ânimo indomável. Ide, então, correi céleres para dentro. (Os filhos de Medeia entram no palácio.) É bem claro, em breve com maior paixão inflamará a nuvem de gemidos que começa a surgir; e que fará, tão malferida, e inaplacável uma alma mordida pela desgraça?

MEDEIA  - Ai! Ai! Sofri, desgraçada, sofri males muito para lamentar.Ó filhos malditos de mãe odiosa, perecei com vosso pai, e a casa caia toda em ruínas. Ama Ai ai de mim, desgraçada! Por que entram as crianças na culpa que é do pai? por que os odeias? Ai, filhos, como eu temo que algo sofrais. Duro é dos soberanos o querer e, pouco mandados, podendo muito, dificilmente mudam suas iras. Melhor é o costume de viver na igualdade; a mim me seja dada velhice tranquila e sem grandezas. Da moderação, vale nome mais que tudo. Dela usar é bem melhor para os mortais; aos homens de nada serve passar tal medida. Maior a pena da desgraça que sofrem, quando em fúria o demônio anda em casa.

(Eurípedes)

Quanto ao gênero textual, Medeia de Eurípedes é um texto dramático. Como provoca, no público, a catarse (forma de purificação e/ou purgação dos sentimentos), Medeia preenche os requisitos de um(a)

Uma professora desenvolveu um jogo para celular com o objetivo de ajudar seus alunos a compreenderem as funções quadráticas. O jogo conta com várias fases em que o jogador deve acompanhar o protagonista em cenários compostos por um par de eixos cartesianos e moedas dispostas em formato de parábola, conforme a ilustração a seguir.

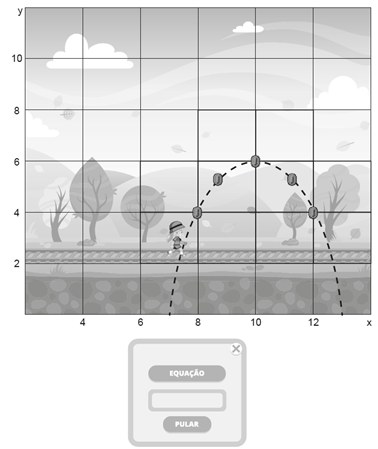
O objetivo do jogador é fazer a personagem pegar as moedas que aparecem ao longo das fases. Para isso, o aluno deve digitar a equação que descreve a parábola formada pela posição das moedas no cenário e, depois disso, acionar o botão “pular” para que a personagem realize a trajetória da parábola. Assim, caso ele acerte a equação, conseguirá capturar todas as moedas que formam a parábola.

Representando-se por y e x os valores dos eixos das ordenadas e das abscissas, respectivamente, a equação que deve ser digitada para que o aluno consiga coletar todas as moedas mostradas na imagem é