Disponível em: https://sites.psu.edu. Acesso em: 12 jun. 2018.

Os recursos usados nesse pôster de divulgação de uma campanha levam o leitor a refletir sobre a necessidade de

O controle de qualidade é uma exigência da sociedade moderna na qual os bens de consumo são produzidos em escala industrial. Nesse controle de qualidade são determinados parâmetros que permitem checar a qualidade de cada produto. O álcool combustível é um produto de amplo consumo muito adulterado, pois recebe adição de outros materiais para aumentar a margem de lucro de quem o comercializa. De acordo com a Agência Nacional de Petróleo (ANP), o álcool combustível deve ter densidade entre 0,805 g/cm³ e 0,811 g/gm³.Em algumas bombas de combustível a densidade do álcool pode ser verificada por meio de um densímetro similar ao desenhado abaixo, que consiste em duas bolas com valores de densidade diferentes e verifica quando o álcool está fora da faixa permitida. Na imagem, são apresentadas situações distintas para três amostras de álcool combustível.

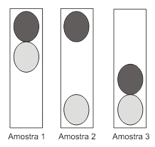
A respeito das amostras ou do densímetro, pode-se afirmar que:

(UNIFESP) O tabuleiro de xadrez persa

Segundo o modo como ouvi pela primeira vez a história, aconteceu na Pérsia antiga. Mas podia ter sido na Índia ou até na China. De qualquer forma, aconteceu há muito tempo. O grão-vizir, o principal conselheiro do rei, tinha inventado um novo jogo. Era jogado com peças móveis sobre um tabuleiro quadrado que consistia em 64 quadrados vermelhos e pretos. A peça mais importante era o rei. A segunda peça mais importante era o grão-vizir – exatamente o que se esperaria de um jogo inventado por um grão-vizir. O objetivo era capturar o rei inimigo e, por isso, o jogo era chamado, em persa, shahmat – shah para rei, mat para morto. Morte ao rei. Em russo, é ainda chamado shakhmat. Expressão que talvez transmita um remanescente sentimento revolucionário. Até em inglês, há um eco desse nome – o lance final é chamado checkmate (xeque-mate). O jogo, claro, é o xadrez. Ao longo do tempo, as peças, seus movimentos, as regras do jogo, tudo evoluiu. Por exemplo, já não existe um grão-vizir – que se metamorfoseou numa rainha, com poderes muito mais terríveis.

A razão de um rei se deliciar com a invenção de um jogo chamado “Morte ao rei” é um mistério. Mas reza a história que ele ficou tão encantado que  mandou o grão-vizir determinar sua própria recompensa por ter criado uma invenção tão magnífica. O grão-vizir tinha a resposta na ponta da língua: era um homem modesto, disse ao xá. Desejava apenas uma recompensa simples. Apontando as oito colunas e as oito filas de quadrados no tabuleiro que tinha inventado, pediu que lhe fosse dado um único grão de trigo no primeiro  quadrado, o dobro dessa quantia no segundo, o dobro dessa quantia no terceiro e assim por diante, até que cada quadrado tivesse o seu complemento de trigo. Não, protestou o rei, era uma recompensa demasiado modesta para uma invenção tão importante. Ofereceu joias, dançarinas, palácios. Mas o grão- -vizir, com os olhos apropriadamente baixos, recusou todas as ofertas. Só desejava pequenos montes de trigo. Assim, admirando-se secretamente da humildade e comedimento de seu conselheiro, o rei consentiu.

No entanto, quando o mestre do Celeiro Real começou a contar os grãos, o rei se viu diante de uma surpresa desagradável. O número de grãos começa bem pequeno: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024... mas quando se chega ao 64o quadrado, o número se torna colossal, esmagador. Na realidade, o número é quase 18,5 quintilhões*. Talvez o grão- -vizir estivesse fazendo uma dieta rica em fibras.

Quanto pesam 18,5 quintilhões de grãos de trigo? Se cada grão tivesse o tamanho de um milímetro, todos os grãos juntos pesariam cerca de 75 bilhões de toneladas métricas, o que é muito mais do que poderia ser armazenado nos celeiros do xá. Na verdade, esse número equivale a cerca de 150 anos da produção de trigo mundial no presente. O relato do que aconteceu a seguir não chegou até nós. Se o rei, inadimplente, culpando-se pela falta de atenção nos seus estudos de aritmética, entregou o reino ao vizir, ou se o último experimentou as aflições de um novo jogo chamado vizirmat, não temos o privilégio de saber.

* 1 quintilhão = 1 000 000 000 000 000 000 = 1018. Para se contar esse número a partir de 0 (um número por segundo, dia e noite), seriam necessários 32 bilhões de anos (mais tempo do que a idade do universo).

(Carl Sagan. Bilhões e bilhões, 2008. Adaptado.)

O trecho “era um homem modesto, disse ao xá” (2º parágrafo) foi construído em discurso indireto. Ao se adaptar tal trecho para o discurso direto, o verbo “era” assume a seguinte forma: